[클러스터링] K-means의 다양한 확장

[거리 혹은 비유사도]에서 이어지는 내용입니다.

0. 내용

1. K-means
2. EM 알고리즘으로 본 K-means
3. 다른 K-centroids 기법들
   1. K-medians
   2. K-modes
   3. K-protypes
   4. Spherical K-means
   5. Minibatch K-means
   6. K-medoids
4. Fuzzy C-means
5. K-means++
6. 경사 하강 최적화
7. 중심점의 개수를 정할 수 있을까? (X-means)
8. 나가며
9. 코드
   1. R
   2. Python

---

1. K-means

    K-means는 가장 유명한 클러스터링 방식이 아닐까 생각이 들 정도로 여러 분야에서 광범위하게 사용되는 클러스터링입니다. 아이디어도 직관적이고 다양한 다른 클러스터링 기법들과 연관도 많아서 그런 것이 아닐까 합니다. 계산도 빠르구요!

    가장 먼저 이야기해야 할 것은 아무래도 목적 함수 (혹은 손실 함수)일 것입니다. 과연 K-means는 무슨 값을 최소화하여서 데이터를 클러스터링 하는 것일까요? 설명에 앞서 노테이션은 다음과 같습니다.

데이터 셋 $X$ 안에는 $N$개의 데이터 포인트 $x_1, \ldots, x_N$이 존재합니다.
$K$개의 중심점(centroids)은 $\mu = \{\mu_1, \ldots, \mu_K\}$로 표현합니다.
$\gamma(x_i, \mu_j)$는 소속 함수로 $x_i$가 $\mu_j$에 속하면 $1$, 속하지 않으면 $0$을 반환하는 함수입니다.

 

이때 목적 함수 $\mathcal{J}$는 다음과 같습니다.

$$ \mathcal{J} = \sum_{k=1}^K{\sum_{n=1}^N{\left[\gamma(x_n,\mu_k)||x_n-\mu_k||^2\right]}} $$

    목적 함수의 의미는 분명합니다. 먼저 하나의 클러스터에 방문해서 그 클러스터에 있는 모든 데이터 포인트와 중심점 사이의 유클리드 거리 제곱을 더한다...그리고 다음 클러스터로 이동하여 동일한 계산을 한다...모든 클러스터에서 계산을 마친 이후에 각 클러스터에서 계산된 값을 모두 더한다는 의미입니다. 그리고 그 값은 최소화되어야 합니다. 한 마디로, 클러스터 안의 유클리드 거리 제곱의 총합이 가장 작은 해법을 찾는 것이 K-means의 목표입니다.

    그렇다면 저 목적 함수를 최소화하는 구체적인 방법은 무엇일까요? 직관적으로 이해하기에 가장 좋은 방법은 그림을 보면서 말로 설명하는 것 같습니다.

    지금부터 K-means 알고리즘이 진행되는 방식에 대해서 알아볼텐데 실제로 학습되는 과정은 아니고 그냥 이해를 돕기 위해 만든 가짜 자료입니다 (실제로는 이렇게 깔끔하게 잘 안 되는 경우도 많습니다). 먼저 우리에게 아래와 같은 데이터가 주어져 있다고 하겠습니다.

클러스터링하기 쉬워 보이는 데이터

이때 K-means 알고리즘은 다음과 같습니다.

 

1. 클러스터 개수를 정한다.
2. 적당한 범위 내에서 각 클러스터의 중심점을 무작위로 생성한다.
3. 수렴할 때까지 아래 두 단계를 반복한다.
   1. 모든 $x \in X$를 유클리드 거리 상 가장 가까운 중심점에 할당한다.
   2. 각각의 중심점에 대해, 중심점에 할당된 데이터의 평균으로 해당 중심점을 업데이트한다.

그리고 이걸 그림으로 보면 다음과 같습니다.

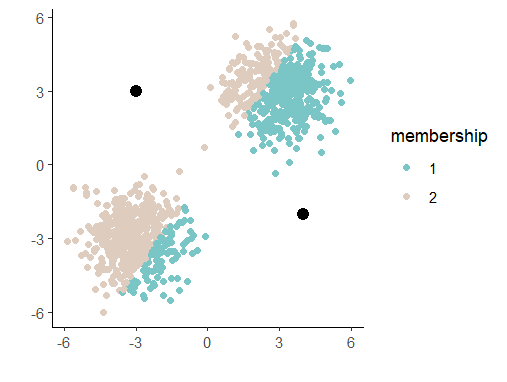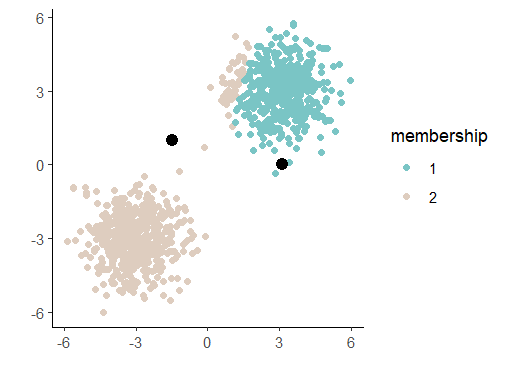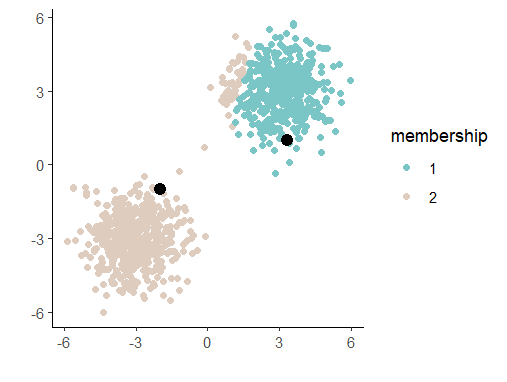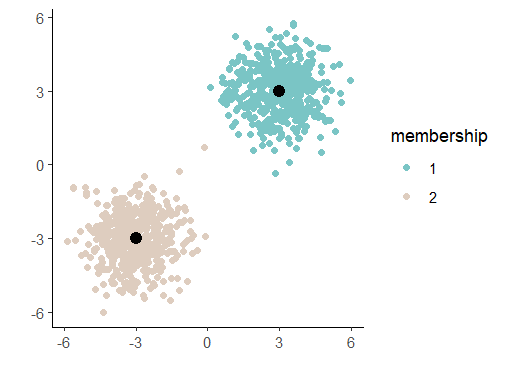
중심점이 제자리를 찾아가는 모습

    사실 여기까지만 이해해도 어디 가서 K-means를 알고 있습니다...!라고 얘기해도 무방하다고 생각합니다.

 

---

 

2. EM 알고리즘으로 본 K-means

    그런데 한 걸음 더 들어가면 이런 의문이 듭니다. '저 알고리즘이 어떻게 목적 함수를 최소화하는 방식으로 작동하는가?' 이를 설명하기 위해 가장 많이 이용하는 방식이 EM (Expectation Maximization) 알고리즘인 듯합니다. 

    EM 알고리즘은 직접 계산해서 가능도를 최대화하기 어려울 때, 알고리즘을 통해 간접적인 방식으로 최대 가능도 추정치를 구하는 방식입니다. 이 글에서는 아주 자세히 적지는 않고 직관적인 수준에서 이해하는 것을 목표로 하겠습니다.

    상황을 상기하자면 우리에게 주어진 데이터는 $X = \{x_1, \ldots, x_N\}$이고 구하고자 하는 파라미터는 $\mu, \gamma$입니다. 그리고 이를 구하기 위해 계산하고 싶은 것은 가능도 $p(X|\mu)$이고, 이를 최대화하는 $\mu$를 구한 뒤에 그걸 기반으로 $\gamma$를 찾는 것이 최종 목적입니다.

    일단, 로그 가능도가 있습니다.

$$ \ln{p(X|\mu)} $$

위의 식에 잠재 확률 변수 $z \in Z$ (여기서는 discrete하다고 가정하고 계산하지만 연속 함수여도 됩니다)를 도입해 보겠습니다. K-means로 따지자면 어떤 하나의 클러스터를 선택하는 변수입니다. 약간 복잡하긴 한데, 조금 더 설명을 하자면 이렇습니다. 전체 클러스터 중에서 하나의 클러스터를 선택할 확률은 그 클러스터 안의 데이터 포인트를 선택할 확률과 같습니다. 즉, 전체 데이터 포인트에서 무작위로 하나를 선택하여 그것이 소속된 중심점을 확인하는 과정이기도 합니다. 다른 말로는, 전체 데이터 중 중심점 1에 속한 것들, 중심점 2에 속한 것들, ...의 비율이 어떻게 되느냐는 말이기도 합니다. 그래서 확률 변수인 것이고 총합은 1입니다. 따라서 데이터의 소속에 의해 결정되는 변수이므로 K-means에서는 소속 함수 $\gamma$와 연관이 되어 있습니다. 아무튼... 이때 로그 가능도를 다음과 같이 적을 수 있습니다. 여기서 $q(Z)$는 $Z$의 분포입니다.

$$ \ln{p(X|\mu)}=\ln{\sum_{z \in Z}{p(X,z|\mu)}} = \ln{\sum_{z \in Z}{q(Z)\frac{p(X,z|\mu)}{q(Z)}}}  $$

그런데, 위의 값은 젠센 부등식에 의해 아래와 같은 성질을 가집니다.

$$ \ln{\sum_{z \in Z}{q(Z)\frac{p(X,z|\mu)}{q(Z)}}} \geq \sum_{z \in Z}{q(Z)\ln{\frac{p(X,z|\mu)}{q(Z)}}} $$

이때 우리는 부등식의 오른쪽, 로그 가능도의 최소값을 하한(lower bound)이라고 부르며, 아래와 같이 노테이션 하겠습니다.

$$ L(q,\mu) :=  \sum_{z \in Z}{q(Z)\ln{\frac{p(X,z|\mu)}{q(Z)}}} $$

    그럼 이제 로그 가능도의 하한이 존재한다는 사실을 알았는데, 로그 가능도와 하한은 얼만큼 차이가 날까요? 재미있게도 쿨백-라이블러 발산만큼 차이납니다 (계산 과정은 시간날 때 추가해 보겠습니다). 따라서 이렇게 적을 수 있습니다. 여기에서 $D_{KL}$은 쿨백-라이블러 발산입니다.

$$ \ln{p(X|\mu)} - L(q, \mu) = D_{KL}(q||p) $$

쿨백-라이블러 발산은 깁스 부등식에 의해 0보다 크거나 같습니다. 따라서 우리가 하한이라고 정한 것이 정말로 하한이었다는 사실을 젠센 부등식 말고 이렇게도 확인해 볼 수 있습니다. 로그 가능도에서 하한을 빼면 0보다 작아질 수 없다는 것은 하한이 로그 가능도보다 크지 않다는 얘기니까요!

    사실 이제 우리는 EM 알고리즘을 실행할 준비를 모두 마쳤습니다. 가장 먼저 무작위로 $\mu$를 정합니다.

    이후에 E-step에서는 로그 가능도를 최대화하는 잠재 변수 $q(Z)$를 구하고 싶습니다. 그런데 로그 가능도를 직접 최대화할 수 없으니 하한을 최대화합니다. 하한은 어디까지 커질 수 있냐면 $D_{KL}$이 최소값인 0이 되는 지점, 즉 로그 가능도와 같은 크기까지 커질 수 있습니다. 따라서 $D_{KL}(q||p)=0$을 만드는 경우인 $p=q$가 우리가 원하는 경우입니다. 이는 자세히 적으면,

$$ q(Z) = p(Z|X, \mu) $$

라고 적을 수 있습니다. K-means의 관점에서 보면 우리가 구하고 싶은 소속 함수 $\gamma$를 로그 가능도가 최대화되는 방향으로 구하기 위해 하한을 증가시켜야 하고, 하한을 증가시키기 위해서는 현재 주어진 데이터 $X$와 현재 주어진 중심점 $\mu$를 기준으로 구한 $\gamma$가 실제 우리가 원하는 분포라고 가정한다...고 말할 수 있습니다. 즉, 현재 주어진 중심점이 맞다고 가정하고 데이터 포인트를 가장 가까운 중심점에 소속시키는 과정입니다.

    다음으로 M-step에서는 로그 가능도를 최대화하는 $\mu$를 구하고 싶습니다. 다시 말해, 이제 중심점을 업데이트하고 싶습니다. 이때는 최대가능도법으로 편미분을 이용해 중심점을 업데이트할 수 있습니다. 업데이트되는 새로운 중심점이 $\mu^{(new)}$라고 하면,

$$ \mu^{(new)} = \arg\max_{\mu}{L(q, \mu)} $$

와 같이 구할 수 있습니다. 목적 함수를 $\mu_k$로 미분하면,

$$ \frac{\partial{\mathcal{J}}}{\partial{\mu_k}} = 2\sum_{k=1}^K{\left[\gamma(x_n,\mu_k)(x_n-\mu_k)\right]}=0 $$

이 나오고, 이를 풀면 $\mu_k$는 현재 $\mu_k$에 할당된 데이터들의 평균이 됩니다. 그러므로 현재 중심점에 할당된 데이터들의 평균으로 해당 중심점을 업데이트합니다.

    정리하자면, E-step은 데이터와 중심점이 고정되어 있다고 생각하고 잠재 변수인 소속 함수를 업데이트한다, 그리고 M-step은 데이터와 잠재 변수가 고정되어 있다고 생각하고 중심점을 업데이트한다...입니다. 그리고 수렴할 때까지 E-M-E-M- ... 계속 반복하는 것이 EM 알고리즘으로 K-means 문제를 푸는 방법입니다.

    그런데 하나 의문이 드는 지점은 과연 하한을 증가시키는 것이 로그 가능도를 무조건 증가시키는가...하는 문제가 있습니다. 직접적으로 로그 가능도를 건드리지 않았는데도 말이죠! 이를 알아보기 위해 원래 파라미터 $\mu$와 업데이트된 파라미터 $\mu^{(new)}$의 로그 가능도 차이에 대해 계산해 보겠습니다.

 

$ \ln{p(X|\mu^{(new)})} -  \ln{p(X|\mu)}  $

 

$ = \ln{\sum_{z \in Z}{\left[p(z|\mu^{(new)})p(X|\mu^{(new)},z)\right]}} - \ln{p(X|\mu)} $ // 잠재 변수를 도입합니다.

 

$ = \ln{\sum_{z \in Z}{\left[p(z|X,\mu) \frac{p(z|\mu^{(new)})p(X|\mu^{(new)},z)}{p(z|X,\mu)}\right]}} - \ln{p(X|\mu)} $ // 시그마 안의 값에 1을 곱합니다.

 

$ \geq {\sum_{z \in Z}{\left[p(z|X,\mu) \ln{\frac{p(z|\mu^{(new)})p(X|\mu^{(new)},z)}{p(z|X,\mu)}}\right]}} - \ln{p(X|\mu)} $ // 로그를 시그마 안으로 넣어서 젠센 부등식을 이용합니다.

 

$ = {\sum_{z \in Z}{\left[p(z|X,\mu) \ln{\frac{p(z|\mu^{(new)})p(X|\mu^{(new)},z)}{p(z|X,\mu)}}\right]}} - \sum_{z \in Z}{p(z|X,\mu)}\ln{p(X|\mu)} $ // $\because \sum_{z \in Z}{p(z|X,\mu)}=1$

 

$ = \sum_{z \in Z}{\left[   p(z|X,\mu)\cdot \ln{\frac{p(z|\mu^{(new)})p(X|\mu^{(new)},z)}{p(z|X,\mu)p(X|\mu)}}   \right]} $

 

가 되고 마지막 결과물을 아래와 같이 노테이션 하겠습니다.

$$ \Delta(\mu^{(new)}|\mu) $$

그렇다면 우리는 다음과 같은 계산을 한 셈이네요.

$$ \ln{p(X|\mu^{(new)})} - \ln{p(X|\mu)} \geq \Delta(\mu^{(new)}|\mu) $$

이때, $\Delta(\mu^{(new)}|\mu)$ 를 최대화하는 방식으로 ($\mu \rightarrow \mu^{(new)}$) 업데이트하면 자연스럽게 로그 가능도는 감소하지 않습니다.

    사실 $\Delta(\mu^{(new)}|\mu)$ 는 위에서 보았던 하한입니다. $\mu^{(new)}$에 대해 하한의 정의를 다시 가져오면,

$$ L(q,\mu^{(new)}) =  \sum_{z \in Z}{\left[ q(Z)\ln{\frac{p(X,z|\mu^{(new)})}{q(Z)}} \right]} $$

입니다. 그리고, E-step에서 $D_{KL}(q||p) = 0$, 즉, $q = p$인 상황을 가정하고 $q(Z) = p(Z|X, \mu)$라고 하면 아래와도 같습니다.

$$ \sum_{z \in Z}{\left[ p(z|X,\mu) \cdot \ln{\frac{p(X,z|\mu^{(new)})}{p(z|X,\mu)}} \right]} $$

이는 풀어 보면, $\Delta(\mu^{(new)}|\mu)$와 같습니다. 결국 하한을 증가시키면 로그 가능도는 감소하지 않는다...는 결론에 도달할 수 있습니다. 하지만 EM 알고리즘은 여느 알고리즘과 비슷하게 global optimum이 아닌 local optimum에 도달하게 됩니다. 따라서 사용할 때마다 다른 결과가 나올 수 있고, 이는 K-means도 똑같습니다.

    이런 식의 클래식한 EM 알고리즘을 K-means에서는 Lloyd 알고리즘이라고 합니다. 그러나 이는 학습이 뭐랄까요... 세밀하지가 않습니다. 그래서 대안으로 나온 것이 MacQueen 알고리즘과 Hartigan-Wong 알고리즘입니다. 이 두 알고리즘은 Lloyd보다 보통은 더 나은 결과를 보인다고 알려져 있습니다. 그리고 아무런 설명 없이 'K-means 알고리즘'이라고 하면 최초 제안자인 MacQueen의 방법을 지칭하는 경우가 대부분입니다.

    MacQueen 알고리즘은 하나의 데이터 포인트를 중심점에 소속시킬 때마다 중심점을 업데이트하는 방식입니다. 아무래도 Lloyd 알고리즘보다 학습할 기회가 더 많습니다. 한 번의 반복에서 중심점 개수만큼 중심점을 업데이트하는 Lloyd에 비해 MacQueen은 데이터 포인트의 개수만큼 중심점을 업데이트하기 때문입니다.

 

1. 클러스터 개수를 정한다.
2. 적당한 범위 내에서 각 클러스터의 중심점을 무작위로 생성한다.
3. 수렴할 때까지 아래 두 단계를 반복한다.
   1. 하나의 데이터 포인트를 가장 가까운 중심점에 할당한다.
   2. 방금 데이터 포인트를 획득한 중심점을 업데이트한다 (중심점에 할당된 데이터의 평균으로).

 

    Hartigan-Wong 알고리즘은 MacQueen보다 더 세밀하고 더 시야가 넓은 방식입니다. 하나의 데이터 포인트를 소속시킬 때마다 모든 중심점과 전체 목적 함수를 고려합니다. 그리고 알고리즘을 시작하기 전에 모든 데이터를 임의의 클러스터에 소속시킨 다음에 데이터 포인트를 하나의 클러스터에서 다른 클러스터로 이동시키는 방식을 사용합니다. 클러스터들이 데이터를 주고 받는다고 해서 이런 방식을 교환 알고리즘(exchange algorithm)이라고도 부르는데, Hartigan-Wong도 교환 알고리즘의 일종입니다. 알고리즘은 아래와 같습니다.

 

1. 클러스터 개수를 정한다.
2. 적당한 범위 내에서 각 클러스터의 중심점을 무작위로 생성한다.
3. 모든 데이터를 중심점에 무작위로 소속시키고, 각 중심점에 속한 데이터 평균으로 중심점을 업데이트한다.
4. 수렴할 때까지 아래를 반복한다.
   1. 하나의 데이터 포인트에 방문.
   2. 방문한 데이터 포인트에서 모든 중심점까지의 소속을 고려한다.
   3. 목적 함수 개선이 가장 큰 소속을 따라 현재 데이터 포인트를 중심점에 할당한다.
   4. 모든 데이터는 어떤 중심점에 속한 상태이므로 소속을 변경하면, 데이터 포인트를 잃은 중심점과 얻은 중심점이 하나씩 생긴다. 이 두 중심점을 업데이트한다.

 

    셋 중에 무엇이 가장 좋아 보이나요? 참고로 R의 기본 패키지인 stats에서 디폴트는 Hartigan-Wong입니다.

 

---

 

3. 다른 K-centroids 기법들

 

3-1. K-medians

    K-means에서는 유클리드 거리를 사용합니다. 하지만 유클리드 거리는 아웃라이어에 민감합니다. 따라서, 아웃라이어에 덜 민감한 맨해튼 거리를 사용하는 방법입니다.

 

3-2. K-modes

    범주형 변수를 다루기 위해 해밍 거리를 사용하는 기법입니다. 범주형 변수의 특성 상 초기 중심점을 정할 때 주어진 범주 안에서 정합니다. 예를 들어, 주어진 변수의 '동물' 축에 '고래', '고양이', '호랑이' 밖에 없는데, 중심점의 '동물' 축을 '이구아나'(!)라고 할 수는 없으니까요. 그렇게 중심점을 정하면 해당 중심점의 '동물' 축은 모든 데이터와 1의 거리를 발생시키기 때문에 사실 상 무시되는 축이 됩니다.

    K-modes 역시 아웃라이어에 민감하다고 여겨집니다.

 

3-3. K-prototypes

    연속형 거리와 범주형 거리를 동시에 이용하는 방법입니다. 이때 특별한 거리를 사용하는데요. 수식을 너무 많이 봐서 피곤하니까 다시 그림으로 돌아와서 예시로 살펴보겠습니다. 아래와 같이 두 차원의 연속형 요소와 두 차원의 범주형 요소를 가지는 두 개의 데이터 포인트 $x_1, x_2$가 있다고 하겠습니다.

데이터 포인트 $x_1, x_2$와 그 사이의 거리

이때 둘 사이의 거리 $d(x_1, x_2)$는 위와 같습니다. 연속형 요소에는 유클리드 거리의 제곱을, 범주형 요소에는 해밍 거리를 사용해서 계산한 이후에 더합니다. 물론 유클리드 거리 제곱과 해밍 거리 이외에 다른 거리 개념을 사용해도 무방합니다. 이렇게 거리 개념을 설정하고 난 이후에 EM 알고리즘으로 최적화합니다.

    그런데 $\pi$는 뭘까요? 저건 범주형 변수에 대한 가중치입니다. 다시 말해, 범주형 요소를 얼마나 많이 고려해서 클러스터링할 것이냐의 문제입니다.  $\pi = 0$이면 범주형 변수를 무시하고 계산하므로 연속형 범주에 대한 K-means가 됩니다. 그렇다면 $\pi$는 어느 정도 되어야 좋은 값일까요? 원 논문에 따르면 연속형 요소들의 표준 편차보다 크지 않은 것이 좋다고 합니다. 하지만 저자 본인도 이는 경험적인 규칙일 뿐이라고 밝히고 있으므로 적절한 값이 있는지는 미지수인 듯합니다. 하이퍼 파라미터 튜닝에 익숙하신 분이라면 한 번 시도해 보시는 것도 좋을 것 같습니다.

 

3-4. Spherical K-means

    Spherical K-means는 유클리드 거리가 아닌 코사인 거리를 이용하는 기법입니다. 그리고 이름에서도 추측할 수 있듯이, 데이터와 중심점의 길이를 계속 정규화하여 1로 만듦으로서 구 위에 올려 두며 학습을 진행합니다. 이외에는 K-means와 다를 게 거의 없습니다. 구체적인 절차는 다음과 같습니다.

    먼저 $K$개의 무작위 중심점을 정합니다. 단, 정한 뒤에는 $L^2$ 정규화하여 모든 중심점 벡터의 길이를 1로 만들어서 단위 원 위에 올려둡니다. 그리고 데이터도 전부 $L^2$ 정규화하여 단위 원 위에 올려둡니다.

    다음으로 E-step에서는 모든 데이터를 가장 가까운 중심점에 소속시킵니다. 이때 사용할 거리는 코사인 거리입니다. 그런데 이미 데이터의 길이를 전부 1로 만들었기 때문에 이런 상황에서는 유클리드 거리를 사용해도 무방합니다. 이전 글에서 보았듯이, $L^2$ 정규화된 벡터 간 유클리드 거리는 코사인 거리 두 배의 루트입니다. 2를 곱하고 루트를 씌워도 대소관계가 바뀌지는 않으니까 가장 가까운 중심점도 바뀌지 않습니다.

    다음으로 M-step에서는 중심점을 업데이트 시킵니다. K-means처럼 소속된 데이터의 평균으로 중심점을 업데이트하면 중심점의 길이가 1이 되지 않아 단위 원에서 탈출할 수 있으니 다른 방법을 사용합니다. 데이터의 총합을 개수로 나누는 것이 아니라, 데이터의 총합을 $L^2$ 정규화하는 것입니다.

    그렇다면 spherical K-means, 과연 어디에 사용하면 좋을까요? 아무래도 방향이 중요한 텍스트 데이터에 많이 사용하곤 합니다.

 

3-5. Minibatch K-means

    기계 학습에 익숙하신 분들이라면 배치를 사용해 보고 싶다...고 생각하실 수도 있습니다. 배치를 사용하는 K-means를 minibatch K-means라고 부릅니다. 이전의 노테이션을 빌려와 적으면 알고리즘은 다음과 같습니다. 여기서 $|.|$는 학습이 진행되는 내내 어떤 중심점이 데이터 포인트를 획득한 횟수의 총합이며, 계수라고 부르겠습니다 (공식적인 용어는 아닙니다).

 

먼저, $|\mu_k| = 0, \forall{k}$라고 계수를 초기화.

1. 반복 횟수(iteration) $T$를 정한다.
2. $T$회 동안 아래의 과정을 반복한다.
   1. 데이터 $X$에서 배치 $B$를 꺼낸다.
   2. 배치 $B$ 안의 모든 데이터에 대해 다음을 반복한다.
      1. 데이터 포인트를 가장 가까운 중심점에 소속시킨다. 여기서는 $x_i$를 $\mu_j$에 소속시켰다고 가정.
      2. $|\mu_j|\leftarrow |\mu_j|+1$  데이터 포인트를 획득한 중심점의 계수를 1 증가.
      3. $\eta = \frac{1}{|\mu_j|}$  학습률 $\eta$를 정한다. 
      4. $\mu_j \leftarrow (1 - \eta) \mu_j + \eta x_i$  중심점을 학습률에 따라 업데이트.

 

    minibatch K-means에서 주목할 만한 점은 학습률이 있다는 것입니다. 학습이 진행될수록 중심점의 계수는 커지고, 중심점에 새로 소속된 데이터가 중심점 업데이트에 더 적은 영향을 주게 됩니다.

    minibatch K-means는 계산이 어려운 큰 데이터를 다루게 해 주는 기법입니다. 그리고 빠르게 수렴합니다. 하지만 학습이 진행될수록 학습률이 낮아져서 중심점이 잘 업데이트되지 않기 때문에, 최초 중심점을 잘못 잡으면 학습 과정에서 수정하기가 어렵습니다.

 

3-6. K-medoids

    medoid는 정의 상 '한 클러스터 안의 모든 데이터 포인트로부터 거리의 총합을 최소화하는 지점'입니다. 어떤 거리냐구요? 아무 거리입니다! 이렇게 말하면 도대체가 이것이 무슨 소리인가...이전의 방식들도 다 medoid 방식 아닌가...싶겠지만, K-medoid는 중심점 최적화를 위해 EM 알고리즘이 아닌 PAM (Partitioning Aroung Medoid) 알고리즘을 사용하는 클러스터링을 의미합니다. PAM은 대단히 간단명료한데, 아래와 같이 진행됩니다.

 

1. BUILD
   1. 클러스터의 개수 $K$를 정한다.
   2. 실제 존재하는 데이터 포인트 중에서 $K$개를 무작위로 선택하여 medoids의 지위를 부여한다.
   3. 모든 데이터를 가장 가까운 medoid에 소속시킨다.
2. SWAP
   1. 모든 medoids에 대해 다음을 반복한다.
      1. 하나의 medoid를 방문한다.
      2. 현재 방문한 modoid에서 medoid가 아닌 모든 데이터 포인트에 일일이 방문하며 medoid 지위를 넘겨줄 때 발생하는 목적 함수의 개선을 계산한다.
      3. 목적 함수가 가장 크게 개선되는 데이터 포인트로 medoid 지위를 넘겨 준다.
      4. 다음 medoid로 이동한다.
      5. 목적 함수를 개선시키는 medoid 이동이 더 이상 없다면 SWAP을 종료한다.
3. 모든 데이터를 가장 가까운 medoid에 소속시키고 알고리즘을 종료한다.

 

    그렇다면 왜 이런 방식을 사용하는 것일까요? 왜냐하면 EM 알고리즘의 수렴이 불안정하기 때문입니다. 보통 EM 알고리즘은 딱히 학습률을 지정하지 않습니다. 그래서 한 iteration에서 중심점이 과도하게 많이 이동할 수 있습니다. 다른 문제로는 EM 알고리즘을 사용하는 K-친구들은 전체 데이터를 확인하며 학습이 진행되지 않습니다. 오히려 딱 현재 중심점에 속한 데이터만 보고 학습하는 근시안이라고 할까요? 반면에 PAM 알고리즘처럼 모든 데이터를 하나하나 빼놓지 않고 꼼꼼하게 살피면서 이동하면 아무래도 보다 안정적인 학습을 기원(🙏🏻)할 수 있습니다. 하지만 너무 꼼꼼하다 보니 시간이 오래 걸려서, 정확도를 약간 포기하고 속도를 높이는 CLARA, CLARANS 기법을 사용하기도 합니다.

 

---

 

4. Fuzzy C-means

    Fuzzy C-means는 K-means에서 소속 함수 $\gamma$가 1 혹은 0이 아니라 $[0, 1]$ 사이의 연속적인 값이라고 보는 기법입니다. 그리고 모든 데이터는 모든 중심점에 속한다고 가정합니다. 단, 얼마나 많이 속하는지에 차이가 날 뿐이죠! 이렇게 데이터가 여러 클러스터에 속하지만, 그 소속도에서 차이가 난다고 가정하는 클러스터링을 soft clustering 혹은 fuzzy clustering이라고 합니다. 그 외에는 K-means와 닮은 점이 많아 이해가 쉬울 것입니다.

    먼저 목적 함수 $\mathcal{J}_c$는 다음과 같습니다.

$$ \mathcal{J}_c = \sum_{k=1}^K{\sum_{n=1}^N{\left[\gamma(x_n,\mu_k)^m \cdot d(x_n,\mu_k)^2\right]}} $$

K-means의 목적 함수와 달라진 점을 보자면,

 

1) $\gamma \in [0,1]$가 연속적이 값입니다.

2) $\gamma$에 가중치인 $m$이 제곱되어 있습니다. $\gamma \in [0,1]$이기 때문에 $m$이 커질수록 $\gamma^m$은 작아지면서 fuzzier한 클러스터링이 됩니다. 그래서 $m$을 fuzzifier라고 부르기도 합니다.

3) 거리 함수가 유클리드 제곱에서 그냥 임의의 거리의 제곱으로 바뀌었습니다 (보통 유클리드 거리를 사용하긴 합니다).

4) 식에 나타나 있지는 않지만, $\sum_{k=1}^K {\gamma(x_n,\mu_k)} = 1, \forall{n}$이라고 가정합니다. 즉, 각 데이터 포인트의 소속도 총합은 1입니다.

 

    이제 학습을 위한 첫 단계로 무작위로 중심점 $\mu$를 지정합니다.

    다음으로 E-step에서 소속을 구하기 위해 목적 함수를 $\gamma(x_n,\mu_k)$로 편미분하면 다음과 같이 정리됩니다.

$$ \gamma(x_n,\mu_k) = \frac{\left( \frac{1}{d(x_n,\mu_k)} \right)^{\frac{1}{m-1}}}{\sum_{k=1}^K{\left( \frac{1}{d(x_n,\mu_k)} \right)^{\frac{1}{m-1}}}} $$

상황을 단순하게 만들기 위해 $m=2$라고 두겠습니다 (실제로도 이렇게 많이들 가정합니다). 이제 의미적으로 식을 보면 꽤나 직관적인 편입니다. 먼저 거리의 역수는 유사도라고 볼 수 있습니다. 즉, $x_n$이 $\mu_k$에 속하는 소속도는 $x_n$이 모든 중심점에 얼마나 가까운지의 총합(분모) 대 $x_n$이 $\mu_k$에 얼마나 가까운지(분자)의 비율입니다. 다시 말해, 다른 중심점에 비해 $\mu_k$에 얼마나 가까운지를 나타낸 식입니다.

    다음으로 M-step에서 중심점을 구하기 위해 목적 함수를 $\mu_k$로 편미분하면 다음과 같이 정리됩니다.

$$ \mu_k = \frac{\sum_{n=1}^N {\left[\gamma(x_n,\mu_k)^m x_n\right]}}{\sum_{n=1}^N {\left[\gamma(x_n,\mu_k)^m\right]}} $$

결국 중심점은 소속도를 가중치로 사용하여 구한, 모든 데이터의 가중 평균입니다.

    정리하자면 Fuzzy C-means의 중요한 특징은 두 가지입니다. 첫째, 소속도를 연속적인 값이라고 생각합니다. 둘째, 모든 데이터가 모든 중심점에 속해 있다고 가정하므로 중심점과 소속도를 학습할 때 전체 데이터를 고려합니다.

    위에서 여러 번 보았듯이, 모든 데이터를 한꺼번에 고려해서 클러스터링하는 방식은 보통 더 안정적이고 더 느립니다. 이는 Fuzzy C-means도 마찬가지입니다.

    만약 soft 클러스터링의 철학이 참 마음에는 드는데 소속 함수는 이산적이면 좋겠다면 데이터 포인트 별로 가장 높은 소속도를 가지는 클러스터에 속한다고 생각하면 됩니다. 한편, 어느 중심점에도 명확하게 속하지 않는 데이터는 노이즈라고 여기고 버리는 것도 생각해 볼 수 있습니다. 여러 모로 쓸모있어 보이네요!

 

 

---

 

5. K-means++

    K-means++는 학습 최초 단계에서 무작위로 생성되는 중심점들을 보다 효과적으로 잡아보기 위해 고안된 방법입니다. 다시 말해, 클러스터링 방법은 아니고 중심점 생성 방법입니다. 왜 이게 필요할까요? 왜냐하면 지금까지 본 K-친구들은 최초 중심점을 어디로 잡느냐에 따라 학습 성능에 차이가 있기 때문입니다. 앞서 EM 알고리즘에서도 보았듯이 우리는 언제나 local optimum에 도달할 뿐이기 때문에 그렇습니다. 특히 최초 중심점들이 우연히 다들 너무 가까이 있으면 학습이 더욱 어려울 것 같습니다.

    그럼 직관적으로 생각해 보면, 최초 중심점들을 서로 멀리 떨어뜨려 놓으면 좋겠습니다. 방법은 이렇습니다. 먼저 데이터 중에 하나의 포인트를 중심점으로 삼습니다. 다음에 그 중심점에서 다음 데이터 포인트로 이동해서 또 중심점을 잡습니다. 이때 중심점에서 데이터 포인트로 이동할 확률은 데이터 포인트까지의 거리에 비례합니다. 멀면 이동할 확률이 높고, 가까우면 이동할 확률이 적습니다. 대단히 직관적이죠!

    그런데 몇 가지 문제가 있습니다. 첫째로, 하나의 중심점을 잡기 위해 모든 데이터 포인트를 고려해야 하니 큰 데이터에서 엄청 오래 걸리는 경우도 있습니다. 결국 K-means의 강력한 장점인 '연산이 빠르다'가 사라져 버리고, 이럴 거면 왜 K-means 쓰나...하는 생각이 들 수 있습니다. 차라리 평범한 K-means를 10번 돌려서 가장 좋은 결과를 보는 게 더 빠를 수 있습니다. 둘째로, 중심점 이동이 바로 이전의 중심점에만 의존하기 때문에 다시 제자리로 돌아올 수 있습니다. 예를 들어, 1 구역에서 멀리 떨어진 2 구역으로는 잘 갔는데, 2 구역에서 가장 먼 곳으로 이동하려고 찾다 보니 다시 1 구역으로 돌아오는 거죠.

    그럼에도 불구하고 K-means++를 시도할 가치는 충분합니다. 첫째 문제에 대해서는, 아주 큰 데이터만 아니라면 요새는 컴퓨팅 파워가 좋아서 그렇게 오래 걸리지는 않습니다. 둘째 문제에 대해서는, 뭐... 무작위 방식보다는 낫지 않을까요? 그래서 실제로 K-means++를 많이 사용합니다. 예컨대, scikit-learn에서는 K-means++가 디폴트입니다. 그리고 다른 많은 패키지에서도 지원합니다.

    K-means++ 이외에도 초기 중심점을 잡는 방법은 다양합니다. 그리고 나름의 방식을 생각해 볼 수도 있습니다. 일단 무작위로 뿌리고 서로 너무 들러붙어 있는 것들만 솎아 내고 다시 뿌리는 것도 방법입니다. 혹은 무작위로 여러 번 생성하고 그 중에서 마음에 드는 것(예컨대 분산이 가장 크다든지 혹은 가장 가까운 두 점 사이의 거리가 가장 크다든지)을 고르는 것도 방법입니다. 혹은 일단 K-means를 실행하고 결과로 나온 중심점을 초기 중심점으로 잡기도 합니다.

 

---

 

6. 경사 하강 최적화

    기계 학습에 익숙하신 분이라면 서두에 K-means의 목적 함수를 보자마자, EM 알고리즘 말고도 경사 하강(GD; gradient descent)을 최적화 가능할 것 같은데...GPU 쓰고 싶은데...라는 생각을 하셨을 수 있습니다. 실제로 가능합니다. 코드는 글이 너무 길어지는 것 같아서 생략하겠습니다. 만약에 쉽게 사용하고 싶으시다면 패키지를 사용하는 것도 방법입니다.

 

---

 

7. 중심점의 개수를 정할 수 있을까? (X-means)

    이 글에 등장하는 모든 클러스터링은 중심점의 개수를 자동으로 추산하지 않기 때문에 분석가가 정해 주어야 합니다. 하지만 우리는 그걸 알 방법이 없습니다. 애초에 몰라서 클러스터링을 하는 것이니까요.

    중심점의 개수를 알고 싶다는 생각은 누구나 하는 생각이기 때문에 수도 없이 많은 사람들이 수도 없이 많은 방법을 제안해 두었습니다. 간단한 방법부터 아주 복잡한 방법까지 다양합니다. 이 글에서는 간단한 가이드라인 정도만 소개할까 합니다.

    첫째는 rule of thumb 방식입니다. 단순무식하게 $K = \sqrt{N/2}$라고 정하는 것입니다. 물론 이게 적절한 값일 가능성은 희박하지만, 정말정말정말로 너무 힌트가 없는 데이터를 만났다면 이 수에서 시작해 보는 것도 방법입니다.

    둘째는 elbow 방식입니다. 요인 분석을 아시는 분이라면 들어봤을 법한 그거 맞습니다. 클러스터의 개수가 증가할수록 목적 함수는 감소하는데, 어느 시점이 되면 목적 함수가 만족스럽게 팍팍 줄어들지 않습니다. 그 지점에서 멈추는 것이 바로 elbow 방식입니다. 다른 말로, 클러스터 개수가 증가할수록 파라미터는 많아지고 과적합(overfitting)이 일어나는데, 과적합이 일어나기 딱 직전의 클러스터 개수를 우리가 원하는 개수라고 보자는 것입니다. 그런데 정말 과적합이 일어나기 딱 직전 상태가 가장 좋은 상태일까요? 사실 그렇다는 보장은 없고 그것이 elbow 방법의 가장 큰 문제입니다.

    혹은 클러스터링만을 위해 만들어진 지표인 실루엣 점수(silhouette score)가 좋은 클러스터 개수를 선택할 수 있습니다. 그런데 실루엣 점수라고 만능은 아닙니다. 제 경험 상 클러스터가 개수가 수십 혹은 백 단위 이상으로 넘어가면 더 잘게 나누어진 많은 클러스터를 선호하는 경향이 있다고 느껴지기는 했습니다 (제 경험이 부족한 것일 수도 있지만요). 이 역시도 과적합에서 아주 자유로울 수는 없는 것 같습니다.

    과적합이 큰 문제라고 느껴진다면 정보 기준(information criterion)들을 사용해 볼 수 있습니다. 예컨대, BIC(Bayesian Information Criterion)이나 AIC(Akaike Information Criterion) 등과 같은 지수들 말이죠! 아무래도 정보 기준은 파라미터의 개수로 가능도를 보정한 형태라 과적합이 된다고 해서 무작정 좋아지지는 않도록 설계되었으니까요. 한 번 써 볼만한 것 같습니다.

    데이터가 충분히 크다면 cross validation을 이용해 볼 수도 있겠네요! train / test로 나누고 train 셋에서의 클러스터링 결과가 test 셋에서 얼마나 적합한지 확인해 보는 것도 방법입니다. 얼마나 적합한지의 지표는 목적 함수나 실루엣 점수 등이 되겠습니다.

    혹은 조금 더 품이 들더라도 여러 번의 다양한 클러스터링 결과가 비슷한 수의 클러스터를 가리킨다는 점을 보여줄 수도 있습니다. 데이터를 다양하게 나누어서 각 subsample마다 다른 클러스터링 기법을 적용했음에도 비슷한 개수에서의 목적 함수가 작다...는 것은 클러스터 개수를 정하는 데에 꽤나 강력한 뒷받침일 수 있습니다 (이러한 방법이 좋은 이유는 망해도 남는 것이 있다는 점도 있습니다. 다양하게 클러스터링 하다 보면 뭔가 데이터랑 친해져서 방법을 찾을지 모르니까요!).

    마지막으로 뭔가 증명해 보려 고생하지 말고 빠르게 포기한 후에 클러스터의 개수를 알아서 추정해 주는 기법을 사용하는 것입니다. 이 글을 중심점 기반 클러스터링을 다루고 있으니, 그 중에 클러스터 개수를 찾아주는 대표적인 기법을 소개하자면 X-means가 있습니다. X-means는 적은 수의 중심점을 정한 뒤에 BIC를 기준으로 중심점을 분할해서 적절한 개수까지 늘리는 방식입니다.

 

---

 

8. 나가며

    지금까지 중심점 기반 클러스터링에 대해 알아 보았습니다. 이 글에서는 기본적인 것 몇 가지만 살펴본 것이라 글에 나온 방법들 외에도 많은 방법들이 있습니다. 혹은 자신의 분석 목적에 적합하다면 기존의 방법을 변용해 보는 것도 좋습니다.

    그럼 다음 글에서는 중심점에 분포를 먹인, 분포 기반 클러스터링에 대해 공부해 보겠습니다.

 

---

 

9. 코드

 

9-1. R

---

K-means

 

    R로 구현한 기본적인 K-means입니다.

    먼저 라이브러리를 불러오고 데이터를 만들어 주는 등 기본적인 세팅을 합니다. kmeans 함수는 R의 기본 내장 패키지인 stats에 들어 있기 때문에 따로 호출할 필요가 없습니다.

### 라이브러리
library(tidyverse)
library(mvtnorm) # to generate multivariate Gaussian data
library(RColorBrewer)

### 기본 세팅
# 시드 설정
set.seed(42)
# 색약을 위한 팔레트 확인. 여기서는 "Set2"를 쓰면 좋겠네요!
display.brewer.all(colorblindFriendly = TRUE)

### 데이터 생성
X = rmvnorm(n = 500, mean = c(0,0)) # 500개의 2차원 표준 가우시안
X = X %>% rbind(rmvnorm(n = 500, mean = c(-12,10)))
X = X %>% rbind(rmvnorm(n = 500, mean = c(10,5)))
X = X %>% rbind(rmvnorm(n = 500, mean = c(-15,-5)))
X = X %>% rbind(rmvnorm(n = 500, mean = c(0,-14)))
X = X %>% rbind(rmvnorm(n = 500, mean = c(23,-14)))
X = X %>% rbind(rmvnorm(n = 500, mean = c(0,16)))
colnames(X) = c("V1", "V2") # 이름도 정해 주고,
X = X %>% as_tibble() # tibble로 만들기!

### 데이터 모양 확인
ggplot(data = X, aes(x = V1, y = V2)) +
  geom_point(color = "grey") + 
  theme_classic()

    아래와 같은 모양입니다.

클러스터링하기 쉬워 보이는 데이터

    이제 K-means를 실행합니다.

### 학습 진행!
km = kmeans(
  x = X,                        # 데이터
  centers = 7,                  # 중심점의 개수
  iter.max = 100,               # 최대 반복 수: 이 안에 수렴하지 못하면 warning
  nstart = 1,                   # 학습 반복 수
  algorithm = "Hartigan-Wong",  # 알고리즘 종류; alternatives: Lloyd, MacQueen
  )

### 아래와 같은 정보들이 생성됨!
km$centers            # 중심점의 좌표
km$totss              # total ss: 거리 제곱의 총합
km$withinss           # ss in each cluster: 각 클러스터 내 거리 제곱 합
km$tot.withinss       # total within ss: 클러스터 내의 거리 제곱 총합
km$betweenss          # between ss: 클러스터 간의 거리 제곱 총합
km$size               # 각 클러스터에 소속된 데이터 수
km$iter               # 수렴할 때까지 사용된 iteration 수
km$cluster            # 각 데이터 포인트의 클러스터 레이블

    이제 결과를 시각화하겠습니다.

### 클러스터 레이블을 원래 데이터에 추가
X %>% add_column(label = as.factor(km$cluster)) -> X_labeled

### 중심점도 데이터 프레임 형태로 만들기
km$centers %>%
  as_tibble() %>% # tibble로 만들어서,
  rowid_to_column("label") %>% # label 정보를 생성
  mutate(label = as.factor(label)) -> centroids # 레이블을 팩터로 변환 후 새로운 변수에 저장

    이제 이를 시각화해 보면!

### K-means 시각화
ggplot(data = X_labeled, aes(x = V1, y = V2, color = label)) +
  geom_point() +
  geom_point(data = centroids, aes(x = V1, y = V2), color = "black", size = 3) +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

낮은 난이도에도 불구하고 망한 K-means

    뭔가 잘 안 되었습니다... 아까 km$iter에서 확인할 수 있듯이 3번만에 수렴했는데 이게 문제일까요? 라이브러리에 강제로 iterations를 늘리는 기능이 없을 뿐더러 늘린다 해도 중심점이 두 개 겹쳐 있는 3, 5번 중심점이 저 자리에서 탈출할 수 있을지는 잘 모르겠습니다. 이럴 때에는 nstart를 100으로 늘려서 서로 다른 초기 중심점을 100개 만들어서 각각에 대해 학습한 이후에 그 중에서 제일 좋은 걸 뽑아서 쓰라고 명령하면 될 것 같습니다.

km = kmeans(
  x = X,                        # 데이터
  centers = 7,                  # 중심점의 개수
  iter.max = 100,               # 최대 반복 수: 이 안에 수렴하지 못하면 warning
  nstart = 100,                 # 초기 중심점 생성 횟수
  algorithm = "Hartigan-Wong",  # 알고리즘 종류; alternatives: Lloyd, MacQueen
  )

    그리고 이 결과를 다시 시각화하면,

성공한 클러스터링!

이번에는 잘 되었네요!

---

K-medians

 

    다음으로는 K-medians입니다. 지금부터는 다양한 K-친구들을 전부 사용할 수 있는 flexclust 라이브러리를 사용하겠습니다. flexclust는 kccaFamily 인자를 받아서 작동합니다. 참고로 flexclust의 기본 최적화 알고리즘은 MacQueen입니다.

### 라이브러리
library(flexclust)
set.seed(42) # 시드

### 학습!
kMedians = kcca(
  x = X, # 데이터
  k = 7, # 중심점 개수
  family = kccaFamily(which = "kmedians"), # 사용할 방법
  )
  
### 학습 결과를 데이터 프레임으로 만들고 tibble로!
kMedians_df = kcca2df(object = kMedians, data = X) %>% as_tibble()

### kMedians_df의 생김새
"
# A tibble: 7,000 x 3
    value variable group
    <dbl> <fct>    <fct>
 1  1.37  V1       5    
 2  0.363 V1       5    
 3  0.404 V1       5    
 4  1.51  V1       5    
 5  2.02  V1       5    
 6  1.30  V1       5    
 7 -1.39  V1       5    
 8 -0.133 V1       5    
 9 -0.284 V1       5    
10 -2.44  V1       5    
# ... with 6,990 more rows
"

결과를 보면 가로 세로축 이름이 variable 변수에 long form으로 들어가 있습니다. 그리고 소속은 group 변수에 저장됩니다. 일단 여기에서 중심점을 뽑아줍니다.

kMedians_df %>% 
  pivot_wider(names_from = variable, values_from = value, values_fn = median) -> kMedians_centroids

그리고 나서는 저 long form인 데이터도 보기 편하게 wide form으로 바꿉니다.

kMedians_df %>%
  group_by(variable) %>% 
  mutate(row = row_number()) %>% 
  pivot_wider(names_from = variable, values_from = value) %>% 
  select(-row) -> kMedians_df

이제 이를 시각화 해 보면,

ggplot(data = kMedians_df, aes(x = V1, y = V2, color = group)) +
  geom_point() +
  geom_point(data = kMedians_centroids, aes(x = V1, y = V2), color = "black", size = 3) +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

역시나 망한 K-medians...

또 망했습니다! 뭔가 건드려 주어야 하겠네요. 이번에는 K-means++ 방식으로 초기 중심점을 생성하는 식으로 문제를 해결해 보겠습니다.

### control을 지정해서 학습!
kMedians = kcca(
  x = X,
  k = 7,
  family = kccaFamily(which = "kmedians"),
  control = list(initcent = "kmeanspp", iter.max = 30000, tolerance = 0.0, verbose = 1),
  )
  
 "
 control 요소 설명
    - initcent = {randomcent: 랜덤(디폴트), kmeanspp: K-means++}
    - iter.max: 알고리즘 최대 반복 수
    - tolerance: 이 값 이하로 변화가 있어야 수렴했다고 판단. 0.0 설정하면 아예 어떠한 변화도 없어야 수렴했다고 판단
    - verbose: 이 값마다 학습 진행 상황 print
 "

이렇게 학습한 것을 위와 같은 과정을 거쳐 시각화 하면 아래처럼 됩니다.

와 성공!

이제 잘 되었네요!

---

Spherical K-means

 

    다음은 spherical K-means입니다. flexclust는 코사인 유사도를 지원하기는 하지만, 중심점을 업데이트할 때 $L^2$ 정규화가 아닌 standardized mean을 사용합니다. 따라서 중심점이 단위 원 위에 있으리라는 법은 없기는 합니다. 그래서 사실 spherical K-means는 아니고 코사인 K-means가 더 어울리는 이름인 것 같기는 한데, 그래도 일단은 해 보겠습니다.

### Spherical K-means
set.seed(42) # 시드!

### 학습
# family에서 "angle"로 지정해서 코사인 유사도 사용
skm = kcca(
  x = X,
  k = 7,
  family = kccaFamily(which = "angle"),
  control = list(initcent = "kmeanspp", iter.max = 10000, tolerance = 0.0, verbose = 1),
  )
# tibble로
skm_df = kcca2df(skm, data = X) %>% as_tibble()
# 평균을 내서 중심점 구하기
skm_df %>% 
  pivot_wider(names_from = variable, values_from = value, values_fn = mean) -> skm_centroids
# long to wide
skm_df %>%
  group_by(variable) %>% 
  mutate(row = row_number()) %>% 
  pivot_wider(names_from = variable, values_from = value) %>% 
  select(-row) -> skm_df

### 시각화
ggplot(data = skm_df, aes(x = V1, y = V2, color = group)) +
  geom_point() +
  geom_point(data = skm_centroids, aes(x = V1, y = V2), color = "black", size = 3) +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

시각화 결과는 아래와 같습니다.

코사인 유사도를 이용한 K-means

각도에 따라서 거리를 계산하니 중심점이 7개는 너무 많은 것 같습니다. 아무래도 6개로 나뉘는 것이 더 합당해 보입니다.

    사실 kccaFamily 인자에 거리 계산과 중심점 업데이트를 위한 custom function을 넣을 수 있습니다. 이번에는 이를 활용해서 진짜 spherical K-means를 해 보겠습니다. 대신에 이번에는 이전 분석에서 교훈을 얻었으니 중심점을 6개로 하겠습니다.

    먼저 다음의 코드를 입력해 보면 kccaFamily에서 angle을 지정했을 때 어떤 계산을 사용하는지 확인할 수 있습니다.

kccaFamily(which = "angle")

"
...
...
Slot "cent":
function (x) 
{
    z <- colMeans(x)
    z/sqrt(sum(z^2))
}
...
...
Slot "preproc":
function (x) 
x/sqrt(rowSums(x^2))
...
...
"

이중에서 cent는 중심점 업데이트에 사용되는 함수인데, standardized mean으로 되어 있으니 이걸 sum의 $L^2$ 정규화로 바꿔주면 됩니다. 그리고 preproc은 전처리 함수인데 데이터를 $L^2$ 정규화하여 단위 원 위에 올려두는 역할을 합니다. 이건 그대로 사용하면 되겠네요! 그리고 거리 계산은 kccaFamily(which = "kmeans")에서 가져와 보겠습니다. 물론 K-means는 유클리드 거리를 사용하지만 앞서 spherical K-means 설명에서 밝혔듯이 유클리드 거리를 사용해도 무방합니다.

kccaFamily(which = "kmeans")

"
Slot "dist":
function (x, centers) 
{
    if (ncol(x) != ncol(centers)) 
        stop(sQuote("x"), " and ", sQuote("centers"), 
            " must have the same number of columns")
    z <- matrix(0, nrow = nrow(x), ncol = nrow(centers))
    for (k in 1:nrow(centers)) {
        z[, k] <- sqrt(colSums((t(x) - centers[k, ])^2))
    }
    z
}
...
...
"

    이제 각 함수를 적절히 사용해서 나만의 kccaFamily를 만들고 학습을 진행합니다.

### Real spherical K-means
set.seed(42) # seed!

### Custom functions
# dist function: Euclidean dist
skm_dist_func = function (x, centers){
  if (ncol(x) != ncol(centers)) 
    stop(sQuote("x"), " and ", sQuote("centers"), 
         " must have the same number of columns")
  z = matrix(0, nrow = nrow(x), ncol = nrow(centers))
  for (k in 1:nrow(centers)){
    z[, k] = sqrt(colSums((t(x) - centers[k, ])^2))
    }
  return(z)
}
# centroid-updating function: L2 normalization
skm_cent_func = function (x){
  z = colSums(x)
  return(z/sqrt(sum(z^2)))
}
# preprocessing: locate the data on unit circle
skm_preproc = function(x){
  return(x/sqrt(rowSums(x^2)))
}

### kccaFamily 정의
skmFam = kccaFamily(dist = skm_dist_func, cent = skm_cent_func, preproc = skm_preproc)

### 학습
real_skm = kcca(
  x = X, 
  k = 6, 
  family = skmFam,
  control = list(initcent = "kmeanspp", iter.max = 10000, tolerance = 0.0, verbose = 1),
  )

### to tibble
real_skm_df = kcca2df(real_skm, data = X) %>% as_tibble()

### long to wide
real_skm_df %>%
  group_by(variable) %>% 
  mutate(row = row_number()) %>% 
  pivot_wider(names_from = variable, values_from = value) %>% 
  select(-row) -> real_skm_df

### centroids
real_skm_df %>%  
  group_by(group) %>% # 클러스터 단위로 묶고,
  summarize(across(everything(), sum)) %>% # 더하기!
  mutate(norm = sqrt(rowSums(across(-group)^2))) %>% # 이후에 group 열을 제외하고 norm을 구해서
  mutate(across(-group, ~ . / norm)) %>% # group 열을 제외한 모든 값을 norm으로 나누어 L2 정규화
  select(-norm) -> real_skm_centroids

### visualization
ggplot(data = real_skm_df, aes(x = V1, y = V2, color = group)) +
  geom_point() +
  geom_point(data = real_skm_centroids, aes(x = V1, y = V2), color = "black", size = 3) +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

이렇게 하면 아래와 같은 결과가 나옵니다.

진짜 spherical K-means

중심점이 $L^2$ 정규화에 의해 단위 원 위에 위치합니다. 나쁘지 않은 결과네요!

 

---

K-modes

 

    이제 이러한 방식으로 kccaFamily에 custom function을 넣어서 온갖 종류의 K-친구들을 실행할 수 있습니다. 그러나 이미 패키지가 있다면 굳이 그래야 할 필요는 없다...고 생각하기 때문에 K-modes와 K-prototypes는 다른 패키지를 사용해 보겠습니다.

    사용할 패키지는 klaR입니다. 먼저 우리가 사용하던 데이터셋에 범주형 데이터가 없으니 만들어서 넣어야겠습니다. 그리고 범주형 변수로만 클러스터링한 이후에 시각화는 연속형 변수로 하겠습니다.

### K-modes
# package
library(klaR)
# klaR은 MASS 패키지를 자동으로 불러오는데, MASS에도 select라는 함수가 있습니다.
# 그래서 우리가 앞으로 사용할 select는 dplyr의 함수라고 정의해 주겠습니다.
select = dplyr::select
# seed!
set.seed(42)

### 새로운 범주형 변수 생성!
# V3: 세로축이 0보다 크면 1, 작으면 0인 변수
# V4: 1사분면이면 1, 이외에는 0인 변수
X %>%
  mutate(V3 = as.logical(V2 >= 0)) %>%
  mutate(V4 = as.logical(V2 >= 0 & V1 < 0)) -> X_mixed

### training
kModes = kmodes(
  data = X_mixed %>% select(V3, V4), # V3, V4만 사용
  modes = 3, # 중심점 개수
  iter.max = 10000, # 최대 반복 수
  )

### 학습 종료까지 소요된 반복 수
kModes$iterations

### 학습된 클러스터를 팩터로 변환해서 원래 데이터에 삽입 후 X_modes로 저장
X %>% add_column(label = as.factor(kModes$cluster)) -> X_modes

### 시각화
# 중심점은 1 or 0이라서 표현하는 것이 의미가 없을 듯
ggplot(data = X_modes, aes(x = V1, y = V2, color = label)) +
  geom_point() +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

결과는 아래와 같습니다. 잘 되었네요!

이번에도 성공!

 

---

K-prototypes

 

    이제 K-prototypes를 해 보겠습니다. 이번에는 'clustMixType' 패키지를 사용하겠습니다. 그리고 중심점 개수는... 연속형 자료로는 7개, 범주형 자료로는 3개니까 도합 10개면 될 것 같습니다. 그리고 범주형 자료에 가중치를 많이 줘 보겠습니다. 가중치는 원래 위에서 보았듯이 연속형 자료의 표준 편차보다 작은 것이 좋지만, 우리는 한... 100 정도 줘 보겠습니다. 우리 마음이니까요! 아래 코드에서 lambda가 범주형 자료에 줄 가중치입니다.

### K-prototypes
library(clustMixType)
set.seed(42)
X_mixed %>% mutate(V3 = as.factor(V3), V4 = as.factor(V4)) -> X_mixed # clustMixType은 factor만 허용

### 학습
# 1 ~ 3분 정도 걸립니다
kp = kproto(
  x = X_mixed, # 데이터
  k = 10, # 중심점 개수
  lambda = 100, # 범주형 자료에 100배 가중치를 줘서
  iter.max = 100000, # 최대 반복 수
  nstart = 100, # 시작점 생성 횟수
  verbose = FALSE, # 이건 시끄러우니까 그냥 끕시다!
  )

### 학습 결과 반영해서 X_proto에 저장
X %>% add_column(label = as.factor(kp$cluster)) -> X_proto

### 시각화
ggplot(data = X_proto, aes(x = V1, y = V2, color = label)) +
  geom_point() +
  theme_classic() +
  scale_color_brewer(palette = "Paired") # Set2는 색이 부족. Paired도 colorblind-friendly입니다.

결과는 아래와 같습니다. 보기에 어떤가요? 연속형 자료와 범주형 자료가 적절히 고려된 결과인 것 같나요? 저는 개인적으로 나름 잘 된 듯합니다.

나름 잘 나뉜 K-prototypes

 

---

Minibatch K-means

 

    이번에는 minibatch K-means입니다. 이번에는 ClusterR 패키지를 사용하겠습니다. 익숙하지 않은 분들을 위해서 MiniBatchKmeans 함수의 파라미터 설명이 필요해 보이네요. batch_size는 한 번의 반복에서 사용할 데이터 포인트의 수입니다. 아래처럼 32이면 32개씩 사용해서 중심점을 업데이트하고, 다음 반복에서 또 다음 32개를 사용해서 중심점을 업데이트하고... 이렇게 하겠다는 이야기입니다. early_stop_iter는 목적 함수의 개선이 이루어지지 않음에도 얼마나 더 반복할지 정하는 파라미터입니다. 학습 중에 목적 함수가 계속 감소하다가 어느 순간부터는 갑자기 증가하는데, 이유는 보통 과적합 때문입니다. 하지만 증가하기 시작한 목적 함수도 몇 번 더 추가적인 반복을 진행하면 다시 감소할 수 있습니다. 다시 말해, 목적 함수가 증가하기 시작했다고 바로 학습을 멈추면 local optimum에 빠질 수 있습니다. 그래서 강제로 학습을 더 반복하면서 정말 더 개선되지 않는 것인지 확인합니다. 물론 가장 최적의 결과물(목적 함수가 가장 작을 때의 결과물)이 저장됩니다.

### Minibatch K-means
library(ClusterR)
mbkm = MiniBatchKmeans(
  data = X, # 데이터
  clusters = 7, # 클러스터 개수
  batch_size = 32, # 배치 사이즈
  num_init = 100, # minibatch K-means를 얼마나 여러 번 실행해서 좋은 값을 뽑을 지
  max_iters = 10000, # 최대 반복 수
  init_fraction = 1.0, # 데이터의 몇 퍼센트나 이용해서 초기 중심점을 생성에 사용할지
  initializer = "kmeans++", # 초기 중심점 생성 방식; alternatives: optimal_init, quantile_init, random
  early_stop_iter = 50, # 목적 함수가 감소하다가 다시 증가하기 시작할 때, 학습을 완료하지 않고 얼마나 더 반복할 지
  verbose = TRUE, # 학습 진행 과정 표시
  tol = 1e-4, # tolerance default
  seed = 42, # 시드를 여기에 넣어줄 수 있습니다.
  )

    Minibatch K-means는 중심점 학습에 전체 데이터를 사용하지 않기 때문에 데이터가 중심점에 소속되지 않습니다. 그냥 중심점만 나올 뿐입니다. 그래서 학습이 끝난 후 데이터를 가장 가까운 중심점에 소속시켜야 합니다.

### 중심점 찾기
mbkm_centroids = mbkm$centroids
colnames(mbkm_centroids) = c(sprintf("V%d", 1:2)) # 이름 정하기!
mbkm_centroids %>% as_tibble -> mbkm_centroids # to tibble


### 가까운 중심점에 할당
# progress bar object
library(progress)
pb = progress_bar$new(total = nrow(X))
# 클러스터 레이블이 들어갈 변수
mbkm_clusters = c()
# 할당!
for(i in 1:nrow(X)){
  data_point = X[i,] # i번째 데이터 포인트
  distances = c() # i번째 데이터 포인트와 j번째 중심 사이의 거리가 저장될 변수
  for(j in 1:nrow(mbkm_centroids)){
    current_centroid = mbkm_centroids[j,] # j번째 중심점을 꺼내서
    Euclidean_dist = sqrt(sum((data_point - current_centroid)^2)) # 유클리드 거리 계산
    distances = c(distances, Euclidean_dist) # 계산된 거리 저장
  }
  current_label = which.min(distances) # 거리가 가장 작은 중심점으로 할당한 이후에,
  mbkm_clusters = c(mbkm_clusters, current_label) # 결과 저장
  
  pb$tick()
}

    이제 시각화를 해 보면!

### 시각화
X %>% add_column(label = as.factor(mbkm_clusters)) -> X_mbkm

ggplot(data = X_mbkm, aes(x = V1, y = V2, color = label)) +
  geom_point() +
  geom_point(data = mbkm_centroids, aes(x = V1, y = V2), color = "black", size = 3) +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

결과는 같습니다.

나름 잘 된듯합니다. 일부 데이터만 가지고 중심점 업데이트를 반복하다 보니 중심점이 분포의 딱 중앙에 있지는 않은 경우도 보입니다.

 

---

K-medoids

 

    다음은 PAM 알고리즘을 사용하는 K-medoids입니다. 이번에는 cluster라는 패키지를 사용하겠습니다.

### K-medoids
library(cluster)
set.seed(42)

### 학습
kMedoids = pam(
  x = X, # 데이터 or 거리 행렬
  k = 7, # 중심점 개수
  diss = FALSE, # x가 거리 행렬이 아니라 데이터라는 뜻
  metric = "euclidean", # 유클리드 거리; alternative: manhattan
  medoids = NULL, # NULL로 지정하면 BUILD 알고리즘에 따라서 시작, 아니면 초기 중심점을 넣을 수 있음.
  stand = FALSE, # 시작 전에 데이터를 표준화할 지
  do.swap = TRUE, # SWAP 알고리즘을 실행하도록, FALSE면 SWAP 없이 BUILD만 사용
  )

### 중심점
kMedoids$id.med # 데이터 중에 어떤 것이 중심점으로 선택되었는지
kMedoids$medoids %>% as.tibble -> kMedoids_centroids
kMedoids_centroids %>% mutate(label = row_number()) -> kMedoids_centroids

### 클러스터 레이블
X %>% add_column(label = as.factor(kMedoids$clustering)) -> X_medoids

### 시각화
ggplot(data = X_medoids, aes(x = V1, y = V2, color = label)) +
  geom_point() +
  geom_point(data = kMedoids_centroids, aes(x = V1, y = V2), color = "black", size = 3) +
  theme_classic() +
  scale_color_brewer(palette = "Set2")

PAM 결과물

    중심점이 주어진 데이터 중에서 결정되기 때문에 정확하게 중심에는 있지 않고-자세히 마음의 눈으로 보면-약간 치우쳐 있기도 합니다.

 

---

Fuzzy C-means

 

    다음은 Fuzzy C-means를 위해 ppclust 패키지를 이용합니다. 여기서는 fuzzy하게 m=10로 두겠습니다. 이전에 설명했듯이 보통 m=2로 많이 두고 이 패키지에서도 이게 디폴트입니다. 그리고 거리는 평범하게 유클리드 거리 제곱을 사용하겠습니다. 앞서 공부한 대로 전체  학습에 시간이 조금 걸립니다. nstart=1으로 제 랩탑에서 2분 정도 걸립니다.

### Fuzzy C-means
library(ppclust)

### 학습!
FuzzyCM = fcm(
  x = X, 
  centers = 7, 
  m = 10, 
  dmetric = "sqeuclidean", # 사용할 수 있는 거리 확인하려면 다음 코드 입력 -> ppclust::get.dmetrics()
  #pw = 2, # the power of Minkowski distance
  alginitv = "kmpp", # K-means++
  nstart = 1, 
  iter.max = 10000, 
  stand = FALSE, # Standardization of the given data: FALSE
  numseed = 42, # random seed
  )

    ppclust 패키지의 fcm 함수는 소속도가 가장 큰 중심점에 데이터를 할당하는 hard clustering 결과도 제공하지만 그러면 뭔가 soft clustering한 의미가 없는 것 같지 않나요? 이번에는 한 클러스터에 대해 소속도가 높으면 더 진하게 표현되는 방식으로 시각화하겠습니다. 아래는 중심점 3, 4에 대한 소속도를 나타낸 시각화입니다. 

### 중심점
FuzzyCM$v %>% as_tibble %>% mutate(lable = row_number()) -> fcm_centroids

### 소속도
cbind(X, FuzzyCM$u) %>% as_tibble -> X_fcm

### 시각화
vis_fcm = function(cluster_label){
  cluster_name = sym(paste("Cluster", cluster_label))
  
  ggplot(data = X_fcm, aes(x = V1, y = V2)) +
    geom_point(aes(color = !!cluster_name)) +
    geom_point(data = fcm_centroids[cluster_label,], aes(x = V1, y = V2), color = "black", size = 3) +
    theme_classic() +
    scale_color_gradient(low = "azure", high = "blue4")
}

vis_fcm(cluster_label = 4)
vis_fcm(cluster_label = 3)

클러스터 3에 대한 소속도

클러스터 4에 대한 소속도

아무래도 분포가 명확하게 나뉘다 보니 fuzzy한 느낌이 확 들지는 않네요.

 

---

클러스터의 개수를 정할 수 있을까?

 

    마지막은 X-means...를 하고 싶었으나 R에서는 마땅히 지원하는 패키지가 없네요. 대신에 클러스터의 개수를 정해주는, 클러스터의 개수를 정하기 위해서만 존재하는 꽤 유명한 패키지인 NbClust를 소개할까 합니다. NbClust 패키지는 NbClust라는 하나의 함수로만 이루어진 쿨한 패키지입니다. 그리고 이 하나의 함수로 26가지 지표를 계산하여 각 지표에 따른 최적의 클러스터 수를 추천해 줍니다. 아무래도 연산이 좀 오래 걸리니까 커피 한 잔 타오시면 됩니다. 제 랩탑에서는 약 6분 정도 걸렸습니다.

nbc = NbClust(
  data = X, # 데이터 
  diss = NULL, # 거리 행렬. 이 부분에 거리 행렬을 넣으려면 아래 거리 계산법이 NULL이어야 함.
  distance = "euclidean", # 거리 계산법
  min.nc = 2, # 탐색할 최소 클러스터 수
  max.nc = 15, # 탐색할 최대 클러스터 수
  method = "kmeans", # 클러스터 방법
  index = "all", # 26 가지 지수 사용. "alllong" 사용 시 30 가지
  )

    위의 변수는 다음과 같은 정보를 담고 있습니다.

nbc$All.index # 최소 ~ 최대 클러스터 수에 대한 각 지표
nbc$Best.nc %>% t # 각 지표가 최적인 클러스터 수와 지표 값
nbc$Best.partition # 최적의 클러스터 수로 클러스터링 한 결과

    결과적으로 클러스터 수 7이 26개 중 11표를 받아서 1등입니다. 하지만 어떻게 보면 너무나도 명확하게 7개로 나뉘는 데이터인데 11표가 좀 적은 것 같기도 합니다. 그래서 이런 패키지를 만들었는지도 모르겠습니다.

 

9-2. Python

    이번에는 기존에 있는 데이터를 사용해 보겠습니다. 데이터는 여기에 있는 데이터를 사용하겠습니다. 먼저 데이터를 개괄합니다.

import pandas as pd

df = pd.read_csv("Mall_Customers.csv")
df.head(3)

	CustomerID	Gender	Age	Annual Income (k$)	Spending Score (1-100)
0	1	Male	19	15	39
1	2	Male	21	15	81
2	3	Female	20	16	6

    Gender를 제외하고는 전부 연속형 변수임을 확인할 수 있습니다. 4, 5열 이름은 사용하기에 불편하니까 바꾸는 것이 좋겠습니다.

df.rename(
    columns={"Annual Income (k$)":"Income", "Spending Score (1-100)":"Spending"},
    inplace=True,
)

    이중에서 우리는 Income과 Spending을 사용해서 클러스터링을 해 보겠습니다. 이 두 변수를 시각화하면 아래와 같습니다.

import matplotlib.pyplot as plt
import seaborn as sns

sns.scatterplot(data=df, x="Income", y="Spending")
plt.show()

소득과 지출의 관계

    5개로 나눠 보는 것을 목표로 하겠습니다.

---

K-means

 

        K-means를 실행하는 패키지는 여러 개가 있습니다. sklearn과 scipy도 제공하죠. 우리는 pyclustering을 사용해 보겠습니다. pyclustering은 사용하기도 꽤 편하고 많은 클러스터링 방식을 지원합니다.

    먼저 데이터를 리스트 형태로 넣어야 하니 리스트 형태로 바꿔 줍니다.

### 데이터를 리스트 형태로 넣어줘야 합니다.
data = df[["Income","Spending"]].values.tolist()

    다음으로 K-means++를 이용해서 초기 중심점을 생성합니다. kmeans_plusplus_initializer가 아닌 random_center_initializer를 사용할 수도 있습니다.

from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer

k = 5 # 목표 클러스터 개수
candidates = kmeans_plusplus_initializer.FARTHEST_CENTER_CANDIDATE # 확률적으로 움직이지 않고 무조건 가장 먼 지점으로 이동
#candidates = 3 # 혹은 3개의 지점을 고려해서 확률적으로 이동
initializer = kmeans_plusplus_initializer(data, k, candidates)
init_centroids = initializer.initialize()

    다음으로 생성된 초기 중심점을 이용하여 K-means를 실행합니다.

from pyclustering.cluster.kmeans import kmeans

kmeans_instance = kmeans(data, init_centroids)
kmeans_instance.process()
clusters = kmeans_instance.get_clusters() # 여기에 소속 정보!
centroids = kmeans_instance.get_centers() # 여기에 중심점!

    pyclustering은 간단한 시각화도 제공합니다. 별로 예쁘지는 않습니다만...

from pyclustering.cluster.kmeans import kmeans_visualizer

kmeans_visualizer.show_clusters(data, clusters, centroids)
plt.show()

꽤나 잘 묶인 K-means

    결과는 나쁘지 않네요!

---

K-medians

 

    이번에는 K-medians입니다. pyclustering 패키지를 사용하기 때문에 코드는 대동소이합니다.

from pyclustering.cluster.kmedians import kmedians

kmedians_instance = kmedians(data, init_centroids)
kmedians_instance.process()
clusters = kmedians_instance.get_clusters()
centroids = kmedians_instance.get_medians()

    시각화하면 아래와 같습니다.

kmeans_visualizer.show_clusters(data, clusters, centroids)
plt.show()

K-medians

---

K-medoids

 

    이번에는 순서를 바꿔서 pyclustering에서 제공하는 기법들부터 전부 수행하도록 하겠습니다. K-medoids도 비슷하게 구현하면 됩니다. 다만 다음 두 가지만 신경 쓰면 됩니다. 1) 존재하는 데이터 포인트 중에 중심점을 고르기 때문에 좌표가 아닌 index가 사용됩니다. 2) 사용할 거리 개념을 설정해야 합니다. 사용 가능한 거리 개념은 여기에서 확인할 수 있습니다.

### 시작할 mdeoids의 indices
import random

init_medoids = random.sample(range(len(data)), k)

### 사용할 거리
from pyclustering.utils.metric import type_metric
from pyclustering.utils.metric import distance_metric

metric = distance_metric(type_metric.MINKOWSKI, degree=2)

### 학습!
from pyclustering.cluster.kmedoids import kmedoids

kmedoids_instance = kmedoids(data, init_medoids, metric=metric)
# run cluster analysis and obtain results
kmedoids_instance.process()
clusters = kmedoids_instance.get_clusters()
medoids = kmedoids_instance.get_medoids()

    결과를 시각화하면 다음과 같습니다.

kmeans_visualizer.show_clusters(data, clusters, [data[x] for x in medoids])
plt.show()

K-medoids

    이번에도 잘 되었네요!

---

X-means

 

    다음은 자동으로 중심점의 개수를 찾는 X-means입니다. 우리는 중심점 3개에서 시작해서 최대 중심점은 20개로 설정하겠습니다.

from pyclustering.cluster.xmeans import xmeans

amount_initial_centers = 3 # Begins with 3 points.
initial_centers = kmeans_plusplus_initializer(data, amount_initial_centers).initialize()

xmeans_instance = xmeans(data, initial_centers, 20) # The centroids can be allocated up to 20.
xmeans_instance.process()

clusters = xmeans_instance.get_clusters()
centroids = xmeans_instance.get_centers()

kmeans_visualizer.show_clusters(data, clusters, centroids)
plt.show()

X-means

    X-means의 선택은 3개네요! 그러나 시드를 고정하지 않으면 6개... 등의 결과도 나오기는 했습니다.

---

K-modes & K-prototypes

 

    다음은 kmodes 패키지를 이용한 K-modes와 K-prototypes입니다. 먼저 Age 변수를 나이대로 범주화한 새로운 데이터 프레임을 만듭니다.

### Numerize Gender column and categorize Age column.
df_categorical = df.copy()
df_categorical["Gender"] = df_categorical["Gender"].apply(lambda x: 0 if x=="Male" else 1)
df_categorical["Age"] = df_categorical["Age"].apply(lambda x: x//10)

    이후에는 아래와 같이 실행하면 됩니다.

### Kmodes
from kmodes.kmodes import KModes

km = KModes(n_clusters=4, init="Huang", n_init=10, verbose=False)
clusters = km.fit_predict(df_categorical[["Age","Gender"]])
print(clusters) # 소속
print(km.cluster_centroids_) # 중심점

### KPrototypes
from kmodes.kprototypes import KPrototypes

kp = KPrototypes(n_clusters=4, init="Huang", n_init=10, verbose=False)
clusters = kp.fit_predict(
    df_categorical.drop(["CustomerID"], axis=1),
    categorical=[0,1], # 어떤 열이 범주형 변수인지!
)

print(clusters) # 소속
print(kp.cluster_centroids_) # 중심점

---

Minibatch K-means

 

    Minibatch K-means는 scikit-learn을 사용하겠습니다.

from sklearn.cluster import MiniBatchKMeans

mbk = MiniBatchKMeans(
    n_clusters=5,
    init="k-means++", # default. The other option is "random"
    max_iter=1_000,
    batch_size=16,
    verbose=0,
    tol=0.0,
    max_no_improvement=20, # Early stopping call
    n_init=10,
    reassignment_ratio=0.01,
)

mbk.fit(data)

    결과를 시각화하면 아래와 같습니다.

ax = sns.scatterplot(data=df, x="Income", y="Spending", color="cornflowerblue")
sns.scatterplot(
    x=mbk.cluster_centers_[:,0], y=mbk.cluster_centers_[:,1],
    color="coral", s=100, marker="s",
    ax=ax,
)
plt.show()

Minibatch K-means

    나쁘지 않은 결과네요!

---

Fuzzy C-means

 

    이번에는 scikit fuzzy 패키지를 사용하겠습니다.

import skfuzzy as fuzz

### 준비!
x = df[["Income","Spending"]].values
c = 5 # 중심점 개수
m = 2 # fuzziness

### 학습!
centroids, u, u0, d, jm, p, fpc = fuzz.cluster.cmeans(x.T, c, m, error=0.005, maxiter=1000, init=None)

"""
centroids: 중심점
u: 소속도
u0: 학습 전 최초 소속도
d: 데이터와 중심점 사이의 거리 행렬
jm: 목적 함수 로그
"""

---

Spherical K-means

 

    Spherical K-means는 별도로 구현되어 있는 패키지는 없습니다. 하지만 원리를 잘 이해하셨다면 이미 구현된 K-means를 이용해서 어렵지 않게 구현할 수 있습니다.

    만약에 단어-문서 행렬을 다룬다면 soyclustering을 사용해 보면 좋습니다. 이런 저런 편리한 기능들이 구현되어 있는 알찬 패키지입니다.